mikioli
Well-Known Member
- 2 770
- 5 387
Dziękuję, że przyznałeś, że osiągnąłem najwięcej z pośród rozkminiającychNo jak na razie jedynym twoim osiągnięciem w tym wątku jest znalezienie rozwiązania zadania w necie..
Dziękuję, że przyznałeś, że osiągnąłem najwięcej z pośród rozkminiającychNo jak na razie jedynym twoim osiągnięciem w tym wątku jest znalezienie rozwiązania zadania w necie..
Ale mówimy o tym... poprzednie miały inny ciężar gatunkowy. Dziwni mnie, wstawienie tego "kosmosu" co teraz, dla zwykłych śmiertelników... A ty od razu pogarda... bo co?Wcześniej były inne zadania, to nie jest pierwsze...
"No, niezły kozak jesteś, znalazłeś rozwiązanie na necie; ciekawe, czy rozumiesz dowódJaka pogarda?
Ale teraz, gdy napisałem, w którym kierunku iść, nie będzie zabawy. Poza tym, musiałbym pomyśleć nad jakimś ciekawym sformułowaniem tego zadania.
ahaTo były tylko przyjacielskie, zaczepne komentarze, a nie jakaś pogarda...
Muszę się zastanowić nad dobrym sformułowaniem, jutro tutaj je napiszę.Jak możesz to wyślij mi na priv, jakiekolwiek sformułowanie tego zadania.
Błędna bo? Podpowiem ci dlaczego tam jest ten link... BO TO TWIERDZENIE DOTYCZY TWOJEGO PRZYKŁADU! ...DżizasO kurczę, nie było mnie trochę czasu i pojawiły się jakieś niestworzone teorie. Dla jasności - odpowiedź mikoliego jest błędna, a zadanie można zrobić w bardzo prosty sposób. Natomiast to twierdza Routh'a to jakaś bardzo uogólniona wersja mojego zadania i może do udowodnienia jego faktycznie potrzeba trochę trudnej teorii. Swoją drogą całe to zamieszanie pokazuje, jak wartościowe są rozwiązania analityczne - nikt nie zdołał wykonać odpowiednich rachunków i zaoponować przeciwko odpowiedzi mikoliego
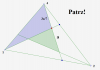
Połóżmy sobie na wierzchołkach trójkąta ciężarki o masie 1, 2 i 4. Zastanówmy się, gdzie leży środek ciężkości takiego trójkąta. Niebieskie punkty to środki ciężkości jego boków (zachowany jest stosunek 2:1). Jeśli szukamy środka ciężkości trójkąta, to dwa ciężarki położone na wierzchołkach możemy zastąpić jednym leżącym w niebieskim punkcie o masie równej sumie mas tych ciężarków. Oczywiście środek ciężkości trójkąta będzie leżał na odcinku łączącym taki niebieski punkt z przeciwległym wierzchołkiem, a zatem musi to być czerwony punkt. Musi również być zachowany odpowiedni stosunek (w przypadku jednego z odcinków 3:4 i drugiego 6:1. Stąd mamy to, co na rysunku. Z twierdzenia Talesa łatwo wynika, że pole niebieskiego trójkąta to 1 (pole dużego) * 2/3 (stosunek odcinków na dolnym boku) * 3/7 (stosunek odcinków na odcinku długości a) = 2/7. Podobnie liczymy pozostałych dwóch trójkątów - wiadomo których.
A zatem pole małego trójkąta to 1 - 3*2/7 = 1/7View attachment 441
EDIT: Teraz zobaczyłem, że w artykule z wikipedii podesłanym przez mikoliego jest odnośnik do artykułu o moim zadaniu.Więc jeśli ktoś chce jeszcze sam pomyśleć, to niech tam nie zagląda.
25/43 sry winetu licz dalejA zadanko dałem, bo skoro była już mowa o robieniu geometrii przy pomocy metod analitycznych i liczb zespolonych, to postanowiłem dać też zadanko na barycentra.Wystarczy, że wezmę ciężarki o masach 1, 7, 49 i zrobię te same rachunki. Tylko wynik tym razem będzie brzydszy, bo 255/399, jeśli dobrze liczę.
Oczywiście masz rację. To co napisałem odnosiłoby się do długości x/8, y/8, z/8. Dla Twojego przykładu należy dać ciężarki o masie 1, 6 i 36. Wówczas pole niebieskiego trójkąta jest równe 1*6/7*7/43=6/43, więc pole zielonego to 1-3*6/43=25/43. Wciąż jest to bardzo szybka metoda na zadania tego typu. Jeśliby stosunki dla boków były różne, to niebieskie trójkąty miałyby różne pola, więc trzeba by było wykonać trzykrotnie więcej obliczeń. Moje pierwotne zadanie jest jednak dużo prostsze i nie wymaga takiego babrania się w rachunkach.25/43 sry winetu licz dalej
Edit. Pominę już jakie cuda by się działy jakby stosunki dla boków były różne...
Też nie prawda bo jeśli już w takim dużym ułamku chcesz to dla x/8 jest 252/399, a po skróceniu ładne 36/57... a nie 255/399. Zresztą mój zarzut jest taki, że logika dorzucania hipotetycznych mas punktowych i cały ten wywód wygląda jakby został przeprowadzony od tyłu... tzn z dobrze rozpracowanym zadaniem innymi metodami. "Dojście" do takiego wywodu jest bardzo trudne in my personal opinion, a że teraz w zasadzie skalujesz równanie, to rzeczywiście może to działać szybkoOczywiście masz rację. To co napisałem odnosiłoby się do długości x/8, y/8, z/8. Dla Twojego przykładu należy dać ciężarki o masie 1, 6 i 36. Wówczas pole niebieskiego trójkąta jest równe 1*6/7*7/43=6/43, więc pole zielonego to 1-3*6/43=25/43. Wciąż jest to bardzo szybka metoda na zadania tego typu. Jeśliby stosunki dla boków były różne, to niebieskie trójkąty miałyby różne pola, więc trzeba by było wykonać trzykrotnie więcej obliczeń. Moje pierwotne zadanie jest jednak dużo prostsze i nie wymaga takiego babrania się w rachunkach.
@tomahawk Jeśli chodzi o książki z różnymi ciekawostkami, ładnymi zadaniami i tp., to moimi ulubionymi są Lilavati i Śladami Pitagorasa Szczepana Jeleńskiego oraz Ostatnie rozrywki Martina Gardnera.
Nie widzę tu złudzenia optycznego - widzę podciągnięty górny bok do wysokości prawego.Są jeszcze schody penrose'a
